Using the PowerShell ISE Editor Object
- Blog
- PowerShell
- Post
In my last article, I introduced you to the PowerShell ISE object model. In the Windows PowerShell ISE, you can view this built-in object by using the following command:
PS C:\> $psise
Where this really gets fun is with the editor. With the editor, you can modify script contents directly from PowerShell. You’ll see why this is useful.
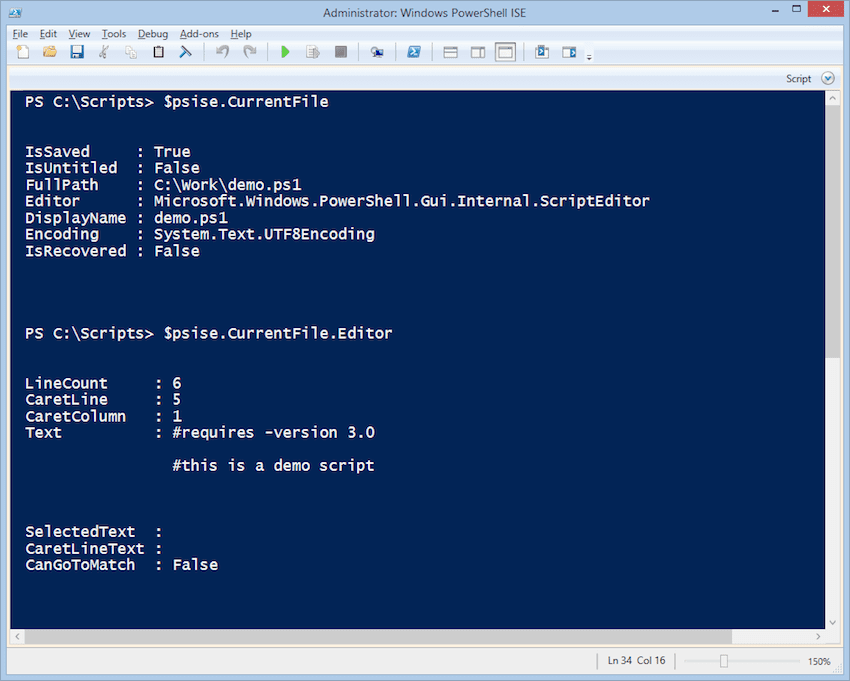
The PowerShell ISE Editor Object
Each ISE file object has an editor property, which is in itself an object.
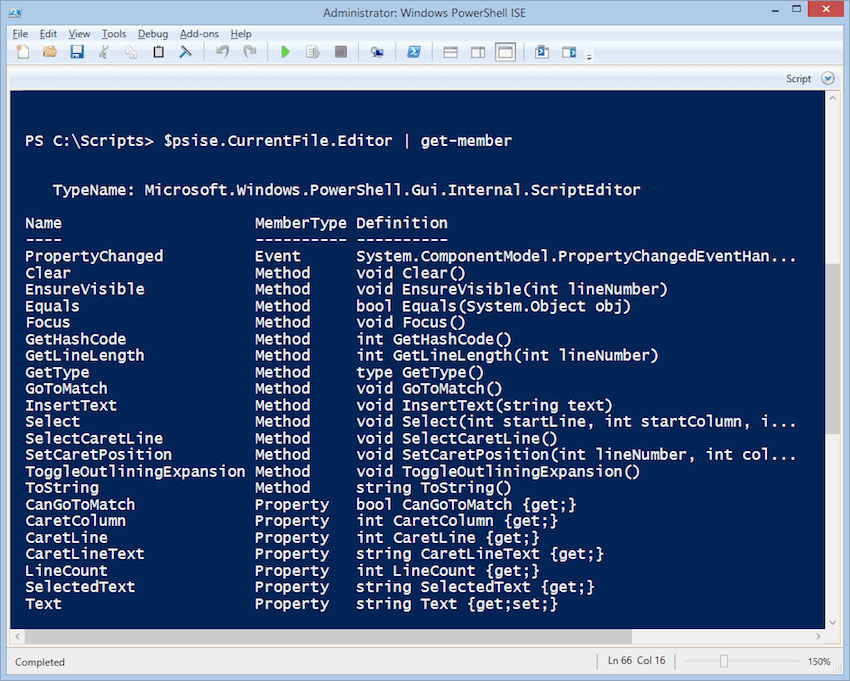
The editor object wouldn’t be much use if you couldn’t do things with it. Pipe the object to Get-Member to discover what it can do.
Inserting Text
Adding text to a file is pretty easy. The following command will insert the comment in the current file at the current cursor location:
PS C:\Scripts> $psise.CurrentFile.Editor.InsertText("#do something interesting here")
You can also move the cursor around. To make things easier, let’s save the editor object to a variable.
PS C:\Scripts> $ed = $PSIse.CurrentFile.Editor
Next, I’m going to move to the last line of the script.
PS C:\Scripts> $ed.SetCaretPosition($ed.LineCount,1)
The SetCaretPosition() method requires parameter values for the line and column numbers, starting at 1. Now I can insert more text.
PS C:\Scripts> $psise.CurrentFile.Editor.InsertText('$Now = Get-Date')
Notice I’m using single quotes for the value. This is so the $Now is not treated as a variable but rather a literal string so that my script now has the line $Now = Get-Date.
Sending output to a tab
You’re probably thinking this is a lot of work when all you have to do is type. And you would be right. But where this gets interesting is when you start building tools around these methods and objects. I have been manually demonstrating some techniques. Creating a tool is where we want to go. For example, I often run a command and want to view the results in a temporary text file. If I’m in the PowerShell ISE, then I can create a new file and insert text using the PSISE model.
Here’s my code.
#requires -version 3.0
Function Out-ISETab { [cmdletbinding()]
Param(
[Parameter(Position=0,Mandatory=$True,ValueFromPipeline=$True)]
$Inputobject,
[string]$Path
)
Begin {
#array to hold all piped object
$data = @()
} #begin
Process {
#add each piped object to the array
$data+=$Inputobject
}
End {
#create a new tab
$newfile = $psise.CurrentPowerShellTab.Files.Add()
#convert data to string and insert into a new ISE Tab
$newfile.editor.InsertText(($data | out-string))
if ($path) {
$newfile.SaveAs($path) }
} #end
}
This function is designed to take pipelined input. The working code is in the End scriptblock when I create a new file and then insert data as text.
PS C:\Scripts> Get-Process | out-isetab
The default is an untitled PS1 file. But I included a Path parameter so you can save the output to a file at the same time.
PS C:\Scripts> Get-Process | out-isetab –path c:\work\myprocs.txt
Now I’m working smarter.
Modifying Scripts
It can be a bit tricky inserting text, especially around existing text, so here is a demonstration script, that you could actually use in the real world. It inserts a comment at the beginning of the script and appends a line at the bottom. The `n characters tell PowerShell to insert a new line.
#Requires -version 4.0 Param([Microsoft.PowerShell.Host.ISE.ISEFile]$File) Write-Host "Modifying $($File.FullPath)" -ForegroundColor Green $top = "#Requires -version 4.0`n`n" $bottom = "`n`n#updated $(Get-Date) by $($env:username)" #jump to the beginning $File.Editor.SetCaretPosition(1,1) #insert a line $File.Editor.InsertText($top) #jump to the last line $File.Editor.SetCaretPosition($file.editor.LineCount,1) #jump to the end of the last line $File.Editor.SetCaretPosition($file.editor.LineCount,$file.Editor.CaretLineText.length+1) #add a line at the end $File.Editor.InsertText($bottom) #save the file $File.Save() #close the file $psise.CurrentPowerShellTab.Files.Remove($File) | Out-Null
With this script I can update any number of files from the ISE.
PS C:\> dir c:\work\*.ps1 | foreach {
$file = $psise.CurrentPowerShellTab.Files.Add($_.FullName)
C:\scripts\Demo-ISEScriptMod.ps1 $file
}
This is a simple example.
The more you experiment with the ISE object model, the more you’ll realize what you can do with it. In the next article, I’ll show you how to incorporate the ISE tools you are developing into the ISE itself.